Wikipedija:Izabrani članci/14, 2013.

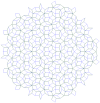
Penroseovo popločenje je aperiodičko popločenje ravnine pločicama koje je proučavao Roger Penrose 1973. S obzirom na to da je aperiodičko, svako je popločenje ravnine ovakvim pločicama neperiodičko. Neperiodičke pločice nemaju translacijsku simetriju, tj. ne postoji dio takva popločenja koji se može pravilno opetovati u svrhu popločenja ravnine. Iako je svako popločenje Penroseovim pločicama neperiodičko, postoje dva popločenja koja posjeduju i zrcalnu simetriju i peterostruku rotacijsku simetriju. Penroseovo popločenje također je dvodimenzionalni kvazikristal, u smislu da stvara oštro obrubljene difraktograme. Postoje dvije popularne inačice Penroseova popločenja koje rabe različite skupove pločica. Robert Ammann neovisno je proučavao popločenje u približno isto vrijeme kad i Penrose.

Godine 1982. Dan Shechtman obznanio je da je uzorak slitine aluminijevog mangana stvorio oštri difraktogram s peterostrukom simetrijom. U isto se vrijeme pretpostavljalo da je takva simetrija nekompatibilna sa sposobnošću difrakcije, s obzirom na to da je peterostruka difrakcija moguća samo u neperiodičkoj strukturi. Potpuno trodimenzionalno slaganje, koje ispoljava ikosaedralnu simetriju, identificirao je Robert Ammann. Atomi su u ravninama koje odgovaraju neobičnoj simetriji poslagani u uzorku Penroseova popločenja. Nicolaas Govert de Bruijn pokazao je da je moguće dobiti Penroseovo popločenje projekcijom iz peterodimenzionalne kubične rešetke. Penroseovo je popločenje s vremenom postalo najizučavaniji i najpopularniji kvazikristal. Zanimanje je fizičara vodilo k drugom pristupu koje je povezalo Penroseovo popločenje s ekstremalnim problemima pri čemu se dokazalo da ono predstavlja model za stanje minimalne energije u nekim sustavima. ...