Rutherfordovo raspršenje

Parametar sudara b i kut skretanja θ.

Datoteka:Pokus s alfa-cesticama 1.jpg

Pokus s alfa-česticama i zlatnim listićem

Gornja slika: Očekivani rezultati: alfa-čestice prolaze kroz Thompsonovog modela atoma.
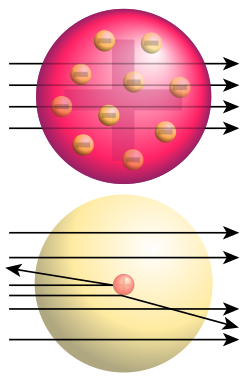
Donja slika: Dobiveni rezultati: samo mali dio alfa-čestice skreće, pokazujući da postoji pozitivan naboj u atomskoj jezgri (treba napomenuti da mjere nisu stvarne, atomska jezgra je još puno manja). To je Rutherfordov model atoma.

Rutherfordovo raspršenje je pojava iz nuklearne fizike, kojom se objašnjava skretanja alfa-čestica koje udaraju u tanke listiće metala, a s njim se dokazuje postojanje pozitivno nabijene atomske jezgre, koja ima gotovo svu masu atoma. Rutherfordovo raspršenje je objašnjenje strukture atomske jezgre, koje je nastalo nakon pokusa s alfa-česticama i zlatnim listićem, kojeg su izveli Ernest Rutherford, Hans Geiger i Ernest Marsden. Rezultati tog pokusa su pokazali da su skretanja alfa-čestica pod velikim kutevima bila jako rijetka, na primjer pri prolazu kroz listić platine na svakih 8000 jedna alfa-čestica bi skrenula pod kutem većim od 90º.

Matematičko objašnjenje

Pokus s alfa-česticama i zlatnim listićem je bio jedan od najznačajnih pokusa u nuklearnoj fizici, jer je to bio prvi dokaz da u atomu postoji atomska jezgra. Na osnovu rezultata mnogobrojnih pokusa, s više različitih metalnih listića, Rutherford i njegovi suradnici su zaključili da pri prolazu kroz kroz metalne listiće nastaje raspršenje ili skretanje alfa-čestica. Ovu pojavu su objašnjavali međusobnim djelovanjem alfa-čestica i jezgre atoma metala, kroz koje su one prolazile.

Rutherford je pretpostavio da do skretanja dolazi zbog djelovanja Coulombove sile ili odbijajuće elektrostatičke sile izmedu alfa-čestica s električnim nabojem Z₁ i jezgre atoma s električnim nabojem Z₂ (Z – atomski broj). Pošto je masa atomske jezgre metala puno veća od mase alfa-čestice, pretpostavka je da je atomska jezgra metala nepokretna. Osim toga, pretpostavka je da elektron ne utječe na skretanje alfa-čestice zbog svoje male mase.

Parametar sudara

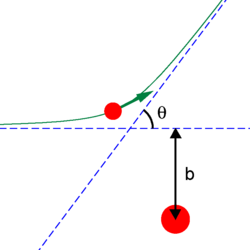
Parametar sudara b je normalna ili okomita (najkraća) udaljenost od centra električno nabijene atomske jezgre do pravca početnog kretanja električno nabijene čestice projektila. Prema Coulombovom zakonu ove dvije čestice s istim nabojem se odbijaju. Odnos između parametra sudara b i kuta skretanja θ iznosi:

[math]\displaystyle{ \theta=\pi-2b\int_{r_\mathrm{min}}^\infty \frac{dr}{r^2\sqrt{1-(b/r)^2-2U/mv_\infty^2}} }[/math]

gdje je: [math]\displaystyle{ v_\infty }[/math] - brzina čestice projektila kada je daleko od centra atomske jezgre i r_min – najkraća udaljenost između centara dviju čestica.

Korištenjem Binetove formule jednadžba putanje alfa-čestice se može opisati:

[math]\displaystyle{ \frac{d^{2}u}{d\theta^{2}}+u=-\frac{Z_{1}Z_{2}e^{2}}{4\pi\epsilon_{0}mv_{0}^{2}b^{2}}=-\kappa, }[/math]

gdje je: [math]\displaystyle{ u={1 \over r} }[/math], [math]\displaystyle{ v_0 }[/math] – brzina čestice projektila kada je daleko od centra atomske jezgre, b – parameter sudara. Rješenje ove diferencijalne jednadžbe je:

[math]\displaystyle{ u=u_{0}\cos(\theta-\theta_{0})-\kappa, }[/math]

za granične uvjete:

[math]\displaystyle{ u\to 0 \quad r\sin\theta\to b \quad(\theta\to\pi). }[/math]

Vrijedi isto:

[math]\displaystyle{ \theta_{0}=\frac{\pi}{2}+\arctan b\kappa. }[/math]

Kut skretanja Θ se može riješiti za [math]\displaystyle{ u\to 0 }[/math] kao:

[math]\displaystyle{ \Theta=2\theta_{0}-\pi=2\arctan b\kappa=2\arctan\frac{Z_{1}Z_{2}e^{2}}{4\pi\epsilon_{0}mv_{0}^{2}b}. }[/math]

Parametar sudara b na kraju iznosi:

[math]\displaystyle{ b=\frac{Z_{1}Z_{2}e^{2}}{4\pi\epsilon_{0}mv_{0}^{2}}\cot\frac{\Theta}{2}. }[/math]

Računanje veličine atomske jezgre

Kod sudara alfa-čestice i atomske jezgre, sva kinetička energija alfa-čestice se pretvara u potencijalnu energiju (Coulombova sila). Zato vrijedi:

[math]\displaystyle{ \frac{1}{2} mv^2 = \frac{1}{4\pi \epsilon_0} \cdot \frac{q_1 q_2}{b} }[/math]

Ili nakon sređivanja:

[math]\displaystyle{ b = \frac{1}{4\pi \epsilon_0} \cdot \frac{2 q_1 q_2}{mv^2} }[/math]

Za alfa-čestice i zlato vrijedi::

• m (masa) = 6,7×10⁻²⁷ kg
• q₁ = 2×(1,6×10⁻¹⁹) C
• q₂ (za zlato) = 79×(1,6×10⁻¹⁹) C
• v (početna brzina alfa-čestice) = 2×10⁷ m/s

Računanjem dobijemo vrijednost oko 2,7×10⁻¹⁴ m (stvarna vrijednost polumjera atomske jezgre zlata je 7,3×10⁻¹⁵ m). Razlika nastaje jer alfa-čestica nema dovoljno energije da dođe toliko blizu atomske jezgre zlata. Pokusi su pokazali da se formule Rutherfordovog raspršenja slažu s rezultatima proračuna, što je dokazalo postojanje atomske jezgre. To je bio uvod u novi Rutherfordov model atoma i dokaz da se Thompsonov model atoma ne slaže s rezultatima pokusa, a time i sa stvarnošću.