Progib
Progib nosača je pomak težišta presjeka u smjeru okomitom na nedeformiranu os nosača (štapa). Kut zaokreta je kut za koji se neki presjek zaokrene u odnosu na svoj prvobitni položaj. Elastična linija nosača ili progibna linija nosača je uzdužna os štapa (težišna linija nosača) u deformiranom (savijenom) obliku. Najveća deformacija nosača ne smije biti veća od unaprijed zadane vrijednosti (uvjet krutosti). Poprečni presjeci pomiču se i istodobno zaokreću oko neutralne osi i pri tome ostaju okomiti na savijenu os štapa. Elastična linija ili progibna linija nosača je savijena (deformirana) uzdužna os nosača. [1]
Progib grede
Jednostavna greda sa silom u sredini
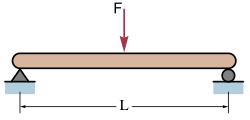
Elastični progib δC (u mm) u sredini jednostavne grede (točka C), koja je opterećena silom F u središtu, a nalazi se na 2 jednostavna oslonca, dat je izrazom:
gdje je:
- = sila koja djeluje u sredini grede (N);
- = duljina između oslonaca (mm);
- = Youngov modul elastičnosti (N/mm2);
- = moment tromosti ili moment inercije (mm4).
Progib u bilo kojoj točki x, uzduž grede, koja je udaljena od jednog oslonca, može se izračunati koristeći jednakost:
za
Jednostavna greda sa silom koja nije sredini
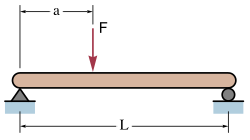
Najveći progib δmax (u mm) jednostavne grede, koja je opterećena silom F koja nije u središtu, a nalazi se na 2 jednostavna oslonca, dat je izrazom:
gdje je:
- = sila koja ne djeluje u sredini grede (N);
- = duljina između oslonaca (mm);
- = Youngov modul elastičnosti (N/mm2);
- = moment tromosti ili moment inercije (mm4);
- = udaljenost sile do najbližeg oslonca (vrijedi ) (mm);
Najveći progib se pojavljuje na udaljenosti od najbližeg oslonca:
Jednostavna greda s kontinuiranim opterećenjem
Elastični progib u sredini jednostavne grede (točka C), koja je opterećena kontinuiranim opterećenjem q (na primjer snijeg - u N/m), a nalazi se na 2 jednostavna oslonca, dat je izrazom:
gdje je:
- = kontinuirano opterećenje (u N/m);
- = duljina između oslonaca (mm);
- = Youngov modul elastičnosti (N/mm2);
- = moment tromosti ili moment inercije (mm4).
Progib u bilo kojoj točki , uzduž kontinuirano opterećene grede je:
Progib konzole

Konzola je konstrukcijski element kojemu je jedan kraj ukliješten u zid (tako da tu nema progiba) ili u koji drugi dio konstrukcije, a drugi mu je kraj slobodan.
Konzola opterećena na slobodnom kraju
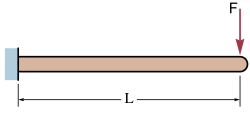
Elastični progib i kut zaokreta (u radijanima) na slobodnom kraju konzole B može se izračunati sa sljedećim izrazom:
gdje je:
- = sila koja djeluje na kraju konzole (N);
- = duljina konzole (mm);
- = Youngov modul elastičnosti (N/mm2);
- = moment tromosti ili moment inercije (mm4).
Treba zapaziti da ako se slobodni kraj konzole poveća za 2 puta, tada se progib poveća za 8 puta. Progib u bilo kojoj točki , uzduž konzole, koja je opterećena na kraju može se izračunati sa sljedećim izrazom:
Kontinuirano opterećena konzola

Elastični progib i kut zaokreta, na slobodnom kraju B, kontinuirano opterećene konzole iznosi:
gdje je:
- = kontinuirano opterećenje nosača (N/m)
- = duljina konzole (mm);
- = Youngov modul elastičnosti (N/mm2);
- = moment tromosti ili moment inercije (mm4).
Progib u bilo kojoj točki , uzduž konzole, koja je kontinuirano opterećena može se izračunati sa sljedećim izrazom:

























