Torzija

Torzija tanke osovine, koja je na jednom kraju pročvršćena za nepokretni oslonac

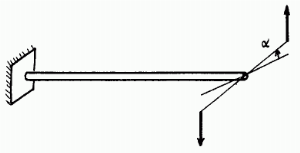
U mehanici čvrstih tijela, torzija predstavlja uvijanje tijela zbog djelovanja momenta. U kružnim presjecima, rezultanta napona smicanja je okomita na radijus.

Napon smicanja na nekom mjestu na osovini je:

[math]\displaystyle{ \tau_{\phi_{z}} = {T r \over J} }[/math]

Važno je napomenuti da je najveći napon smicanja na mjestu gdje je radijus maksimalan, tj. na površini osovine. Visoki naponi na površini mogu se izračunati pomoću koncentracija napona. Zbog toga, osovine koje su jako napregnute na torziju se poliraju do visoke finoće kako bi se smanjio maksimalni napon u osovini i time povećao vijek trajanja osovine.

Kut uvijanja se nalazi pomoću:

[math]\displaystyle{ \phi_{} = {T L \over JG} }[/math]

gdje je:

• r udaljenost od centra rotacija
• Φ ugao uvijanja u radijanima
• T moment(N·m)
• L dužina predmeta na kojeg djeluje moment
• G modul klizanja, koji je obično dat u gigapaskalima (GPa)
• J torziona konstanta za presjek. Jednaka je polarnom momentu inercije za oblu osovinu ili za koncentričnu cijev. Za ostale oblike J se mora odrediti na drugi način.

Polarni moment inercije

Podrobniji članak o temi: Polarni moment inercije

Polarni moment inercije za čvrstu osovinu je:

[math]\displaystyle{ J = {\pi \over 2} r^4 }[/math]

gdje je r radijus predmeta.

Polarni moment inercije za cijev je:

[math]\displaystyle{ J = {\pi \over 2} (r_{v}^4 - r_{u}^4) }[/math]

gdje su u i v (u indeksu) vanjski i unutrašnji radijus cijevi.

Za tanki cilindar:

J = 2π R³ t

gdje su R srednja vrijednost vanjskog i unutrašnjeg radijusa, a t debljina stijeke (zida) tankog cilindra.

Načini otkazivanja

Smicajni napon u osovini može se prikazati kao principalni napon preko Mohrovog kruga. Ako je osovina opterećena samo torzijom tada će jedan od napona biti istezanje, a drugi pritisak. Ovi naponi se orijentirani pod kutom od 45° po obimu osovine. Ako je osovina napravljena od krhkog materijala, tada će osovina otkazati zbog pukotine koja se pojavljuje na površini, a širi prema centru osovine pucajući pod kutom od 45°. Ovo se lako može pokazati uvijanjem školske krede prstima u dva suprotna smjera.