Vigenèreova šifra

Vigenèreova šifra je metoda šifriranja abecednog teksta korištenjem serije Cezarovih šifri, zasnovanih na slovima ključa. Ovo je jednostavni oblik šifre polialfabetske zamjene.

Vigenèreova šifra je otkrivana više puta. Metodu je prvi opisao Giovan Battista Bellaso; međutim, poslije, u 19. stoljeću ta je shema pogrešno pripisana Blaiseu de Vigenèreu, tako da je sad poznata kao "Vigenèreova šifra".

Šifra je dobro poznata zato što, iako je laka za razumijevanje i primjenu, početnicima izgleda kao neprobojna; tako je i dobila epitet fr. le chiffre indéchiffrable - neprobojna šifra. Stoga su mnogi pokušavali primijeniti sheme šifriranja, koje su u osnovi Vigenèreova šifra^[1].

Povijest

Prva polialfabetska šifra, koju je napravio Leon Battista Alberti oko 1467. godine, koristila je metalnu šifarsku ploču za zamjenu šifarskih alfabeta. Albertijev sustav je mijenjao alfabete nakon nekoliko riječi, a zamjena je označavana slovom odgovarajućeg alfabeta u šifratu. Kasnije, u svom djelu Polygraphia iz 1508.^[2] Johannes Trithemius izumio je kvadratnu tablicu (tabula recta), ključnu komponentu Vigenèreove šifre. Međutim, on je dao samo rastući, krut i predvidljiv sustav zamjene šifarskih alfabeta.

Ono što je sada poznato pod imenom Vigenèreove šifre prvobitno je opisao Bellaso 1553. u svojoj knjizi La cifra del. Sig. Giovan Battista Bellaso. Napravio je prema Trithemiusovoj tablici, ali je dodao ponavljajući ključ za promjenu šifarskog alfabeta za svako slovo.

Blaise de Vigenère 1586. objavio je svoj opis slične, ali jače šifre s "autoključem" na dvoru Henrika III. (kralj Francuske i Poljske). Poslije, u 19. stoljeću, pronalazak Bellasoove šifre je pogrešno pripisan Vigenèreu. David Kahn, u svojoj knjizi The Codebreakers - Razbijači kodova, kaže da je povijest "ignorirala ovaj važan doprinos i nazvala regresivnu i osnovnu šifru po njemu [Vigenèreu], iako on ništa nema s tim".^[3]

Vigenèreova šifra je stekla reputaciju kao izuzetno jaka. Poznati pisac i matematičar Charles Lutwidge Dodgson (poznatiji kao Lewis Carroll) nazvao je Vigenèreovu šifru neprobojnom u svom djelu iz 1868. The Alphabet Cipher' - Alfabetska šifra. Časopis Scientific American je 1917. opisao Vigenèreovu šifru kao "nemoguća za prijevod".^[4] Ova reputacija je nezaslužena, jer je Kasiski još u 19. stoljeću potpuno razbio šifru, a poznato je da su je neki kriptoanalitičari povremeno razbijali još u 16. stoljeću.^[3]

Vigenèreova šifra je dovoljno jednostavna za poljsku upotrebu ako se koristi u sprezi sa šifarskim diskovima.^[5] Konfederacija, na primjer, koristila je brončane šifarske diskove za primjenu Vigenèreove šifre za vrijeme Američkog građanskog rata. Poruke Konfederacije su bile daleko od tajne i Unija je redovito razbijala njihove poruke. Za vrijeme rata, vođe Konfederacije prvenstveno su se oslanjale na tri ključa, Manchester Bluff, Complete Victory, Come Retribution (ova posljednja pri kraju rata).^[6]

Gilbert Vernam je pokušao popraviti razbijenu šifru (kreirajući Vernam-Vigenèreovu šifru 1918.), ali i bez obzira na to, šifra je za kriptoanalitičare i dalje bila ranjiva. Međutim, Vernamov rad je doveo do "jednokratnog bloka" (en. one-time pad), provjereno neprobojne šifre.

Opis

Kod Cezarove šifre, svako slovo alfabeta se pomjera za neki broj mjesta; na primjer, sa pomakom 3, slovo A postaje D, B postaje E itd. Vigenèreova šifra se sastoji od niza nekoliko Cezarovih šifara s različitim pomacima.

Za šifriranje se može koristiti tablica alfabeta, nazvana tabula recta, Vigenèreova tablica ili Vigenèreov kvadrat. Sastoji se od alfabeta napisanog 26 puta u novom redu, svaki red rotiran ulijevo u odnosu na prethodni, odgovarajući svim mogućim kombinacijama (26) Cezarove šifre. U pojedinoj točki procesa šifriranja, šifra koristi drugi alfabet iz jednog od redova. Koji će se red koristiti zavisi od ponavljajućeg ključa.

Na primjer, recimo da je otvoreni tekst koji treba šifrirati:

ATTACKATDAWN

Osoba koja šalje poruku bira ključ i ponavlja ga onoliko puta koliko je potrebno da odgovara dužini otvorenog teksta, npr, ključ LEMON:

LEMONLEMONLE

Prvo slovo otvorenog teksta A se šifrira koristeći alfabet iz reda L, koje je prvo slovo ključa. To se radi tako što se traži slovo u redu L i stupcu A Vigenèreove tablice, odnosno traženo slovo je L. Za sljedeće slovo otvorenog teksta se koristi sljedeće slovo ključa, slovo u presjeku reda E i stupca T je traženo slovo X. Po tom sustavu se nastavlja do kraja otvorenog teksta:

Otvoreni tekst: ATTACKATDAWN
Ključ:          LEMONLEMONLE
Šifrat:         LXFOPVEFRNHR

Dešifriranje se vrši traženjem mjesta šifriranog slova u redu tabele, a kao slovo otvorenog teksta se uzima naslov stupca. Na primjer, u redu L, šifrovano L se nalazi u stupcu s naslovom A, koji se uzima kao prvo slovo otvorenog teksta. Sljedeće slovo se dešifruje traženjem slova X u redu E - ono se nalazi u stupcu T i to je traženo slovo otvorenog teksta.

Vigenèreova šifra može se predstaviti i algebarski. Ako se slovima abecede A do Z dodijele vrijednosti 0 do 25 i izvrši sabiranje po modulu 26, šifriranje se može napisati kao

S_{i}\equiv O_{i}+K_{i}{\pmod {26}}

a dešifriranje kao

O_{i}\equiv S_{i}-K_{i}{\pmod {26}}

(O - otvoreni tekst, S - šifrat, K - ključ)

Kriptoanaliza

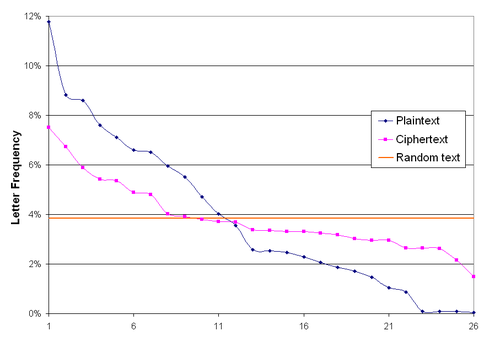
Snaga Vigenèreove šifre, kao i svih polialfabetskih šifara je njena sposobnost otežavanja frekvencijske analize. Frekvencijska analiza je vještina dekriptiranja poruke brojanjem frekvencije slova šifrata i upoređivanje s frekvencijom slova normalnog teksta. Na primjer, ako se slovo K javlja najveći broj puta u šifratu čiji je otvoreni tekst na hrvatskom, može se pretpostaviti da K odgovara slovu A, jer je slovo A najčešće u hrvatskom jeziku. Korištenjem Vigenèreove šifre, slovo A će se zamjenjivati različitim slovima alfabeta na različitim mjestima u poruci i tako onemogućiti jednostavnu frekvencijsku analizu.

Osnovna slabost Vigenèreove šifre je njen relativno kratak i ponavljajući ključ. Ako kriptoanalitičar otkrije dužinu ključa, onda se šifrat može smatrati serijom Cezarovih šifri, koje se zatim pojedinačno jednostavno razbijaju. Testovi Kasiskog i Friedmana pomažu u određivanju dužine ključa.

Kasiskijev test

Friedrich Kasiski je 1863. prvi objavio uspješan napad na Vigenèreovu šifru, ali Charles Babbage je još 1854. razvio isti test. Na razbijanje Vigenèreove šifre Babbage je bio potaknut kad je John Hall Brock Thwaites objavio "novu" šifru u časopisu Journal of the Society of the Arts: kad je Babbage objavio da je to samo još jedna varijanta Vigenèreove šifre, Thwaites se razljutio i izazvao Babbagea da razbije šifru. Babbage je uspio dekripirati uzorak, za koji se ispostavilo da je pjesma "Vizija grijeha" Alfreda Tennysona, a korišten je ključ "Emily", ime Tennysonove žene.^[7].

Test Kasiskog koristi činjenicu da će pojedine česte riječi vjerojatno biti šifrirane istim slovima ključa, pa će se u šifratu pojaviti ponovljene grupe slova. Na primjer, poruka šifrirana ključem ABCDEF neće istovjetno šifrirati crypto svaki put kad se pojavi u otvorenom tekstu:

Ključ:     ABCDEF AB CDEFA BCD EFABCDEFABCD
Otvoreno:  CRYPTO IS SHORT FOR CRYPTOGRAPHY
Šifrat:    CSASXT IT UKSWT GQU GWYQVRKWAQJB

Šifrat u ovom primjeru nema ponovljene nizove slova koji odgovaraju ponovljenim nizovima otvorenog teksta. Međutim, ako je dužina ključa različita, kao u ovom primjeru:

Ključ:     ABCDAB CD ABCDA BCD ABCDABCDABCD
Otvoreno:  CRYPTO IS SHORT FOR CRYPTOGRAPHY
Šifrat:    CSASTP KV SIQUT GQU CSASTPIUAQJB

onda je Kasiskijev test efikasan. Kod dužih poruka je test točniji, jer obično sadrži više ponovljenih segmenata. Sljedeći šifrat ima nekoliko ponovljenih segmenata i omogućuje kriptoanalitičaru da otkrije dužinu ključa:

Šifrat: DYDUXRMHTVDVNQDQNWDYDUXRMHARTJGWNQD

Rastojanje između ponovljenog DYDUXRMH je 18. Stoga, pretpostavljajući da ponovljeni segmenti predstavljaju ponovljene segmente otvorenog teksta, nagovještava da ključ ima dužinu od 18, 9, 6, 3 ili 2 znaka. Razmak između NQD je 20 znakova. To znači da bi dužina ključa mogla biti 20, 10, 5, 4 ili 2 znaka (svi djelioci rastojanja su moguće dužine ključa - ključ dužine 1 je obična šifra pomeranja, gde je kriptoanaliza mnogo jednostavnija). Korištenjem presjeka ova dva skupa, može se zaključiti da je dužina ključa (gotovo sigurno) 2. Naravno, u praksi se nikad neće koristiti ključ dužine 1 ili 2, ovdje je naveden samo radi ilustracije.

Friedmanov test

Ovaj test (poznat i kao "Kapa test") je 1920. otkrio William F. Friedman. Friedman je za razbijanje šifre upotrijebio indeks podudarnosti (en. index of coincidence - I.C.), koji mjeri neravnomjernost frekvencije slova šifre. Ako znamo vjerojatnost $\kappa _{p}$ da u dva nasumice izabrana teksta slova budu ista (za engleski oko 0,067) i vjerojatnost podudaranja nasumične selekcije alfabeta $\kappa _{r}$ (1/26 = 0.0385), dužina ključa se može odrediti kao

${\kappa _{p}-\kappa _{r}} \over {\kappa _{o}-\kappa _{r}}$

iz uočene mjere podudarnosti

$\kappa _{o}={\frac {\sum _{i=1}^{c}n_{i}(n_{i}-1)}{N(N-1)}}$

gdje je $c$ veličina alfabeta (26), $N$ je dužina teksta, a $n_{1}$ do $n_{c}$ su frekvencije slova šifrata.

Ovo je samo aproksimacija čija točnost se povećava s dužinom teksta. U praksi će se probati različite dužine ključeva bliske procjenjenoj.^[8] Bolji pristup za šifre s ponovljenim ključem je da se šifrat kopira u tabelu koja ima onoliko stupaca kolika je pretpostavljena dužina ključa, a zatim da se za svaki stupac posebno izračuna indeks podudarnosti; kad se to uradi za svaku moguću dužinu ključa, najveći prosječni I.C. će odgovarati vjerojatnoj dužini ključa.^[9] Takav test može se dopuniti podacima iz Kasiskijevog testa.

Frekvencijska analiza

Kad se odredi dužina ključa, šifrat se dijeli u odlomke tako da svaki odlomak odgovara ključu za jedno slovo. Svaki dio je ekvivalentan šifratu jedne Cezarove šifre. Pomaci su određeni slovima ključa. Dalje se koristi metoda kojom se razbija Cezarova šifra.

Inačica Kasiskijevog testa je Kerckhoffsova metoda, određivanje ključa dedukcijom na temelju frekvencije riječi u usporednim šifratima.^[10]

Inačice

Inačica Vigenèreove šifre uzastopni ključ (en. running key) je također nekad smatrana kao neprobojna. Ova inačica kao ključ koristi blok teksta dužine otvorenog teksta. Pošto je ključ dugačak kao i poruka, testovi Kasiskog i Friedmana više ne vrijede - ključ se ne ponavlja. Friedman je 1920. prvi otkrio slabost ove inačice. Problem kod Vigenèreove šifre s uzastopnim ključem je što kriptoanalitičar ima statističke informacije o ključu (pod pretpostavkom da je blok teksta iz poznatog jezika) i ta osobina će se odraziti u šifratu.

Ako se rabi ključ koji je potpuno slučajan, ako je dugačak kao poruka i rabi se samo jednom, Vigenèreova šifra je teoretski neprobojna. U tom slučaju ključ, a ne šifra, osigurava kriptografsku otpornost, i ti sustavi se zajednički zovu "jednokratni blok" (en. one-time pad), nevezano za to koja šifra je primijenjena.

Vigenère je, u stvari, otkrio jaču šifru — šifru s autoključem, iako je njegovo ime vezano za jednostavniju polialfabetsku šifru. Te dvije šifre se često mješaju, a obje su nekad imale epitet fr. le chiffre indéchiffrable. Babbage je, u stvari, razbio jaču šifru s autoključem, dok se Kasiskom načelno daje zasluga za prvo objavljeno rješenje polialfabetske šifre s fiksnim ključem.

Otvoreno: SASTANAKUPODNE
Ključ:    KLJUC
Autoključ: KLJUCSASTANAKU
Šifrat:   CLBNCFACNPBDXY

Jednostavnija inačica je da se šifriranje izvodi po metodi dekripcije Vigenèreove šifre, a dekriptiranje korištenjem šifriranja, metoda koja je poznata kao "Beaufortova varijanta" (Ser Francis Beaufort): S = K – O, a dešifriranje kao O = K – S, uz korištenje tzv. Sestrijeve tablice:

   A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
Z  Z Y X W V U T S R Q P O N M L K J I H G F E D C B A
Y  Y X W V U T S R Q P O N M L K J I H G F E D C B A Z
.  . . . . . . . . . . . . . . . . . . . . . . . . . .
A  A Z Y X W V U T S R Q P O N M L K J I H G F E D C B

Usprkos očiglednoj jačini, Vigenèreova šifra u Europi nije bila u širokoj upotrebi. Gronsfeldova šifra je inačica koja je identična Vigenèreovoj šifri, osim što koristi 10 šifarskih alfabeta (koji odgovaraju znamenkama 0 do 9). Šifra je pojačana jer ključ nije riječ, ali je oslabljena jer koristi samo 10 šifarskih alfabeta. Usprkos toj slabosti, Gronsfeldova šifra bila je u širokoj upotrebi u Njemačkoj i u Europi.

Vidi još

Glosar kriptologije

Izvori

↑ Smith, Laurence D. (1943). "Substitution Ciphers". Cryptography the Science of Secret Writing: The Science of Secret Writing. Dover Publications. str. 81. ISBN 048620247X
↑ Trithemius je djelo završio 1508. a knjiga je objavljena 1518.
↑ ^3,0 ^3,1 David, Kahn (1999). "On the Origin of a Species". The Codebreakers: The Story of Secret Writing. Simon & Schuster. ISBN 0684831309
↑ Knudsen, Lars R. (1998). "Block Ciphers— a survey". Unutar Bart Preneel and Vincent Rijmen. State of the Art in Applied Cryptography: Course on Computer Security and Industrial Cryptograph Leuven Belgium, June 1997 Revised Lectures. str. 29. ISBN 3540654747
↑ Codes, Ciphers, & Codebreaking (The Rise Of Field Ciphers)
↑ David, Kahn (1999). "Crises of the Union". The Codebreakers: The Story of Secret Writing. Simon & Schuster. str. 217-221. ISBN 0684831309
↑ Singh, Simon (1999). "Chapter 2: Le Chiffre Indéchiffrable". The Code Book. Anchor Book, Random House. str. 63–78. ISBN 0-385-49532-3
↑ Henk C.A. van Tilborg, ed. (2005). Encyclopedia of Cryptography and Security (First edition ed.). Springer. str. 115. ISBN 038723473X
↑ Mountjoy, Marjorie (1963). "The Bar Statistics". NSA Technical Journal VII (2,4) Published in two parts.
↑ "Lab exercise: Vigenere, RSA, DES, and Authentication Protocols" (PDF). CS 415: Computer and Network Security. http://courses.umass.edu/cs415/labs/lab1/415-lab1-crypto.pdf Pristupljeno 10. studeni 2006.

Vanjske poveznice

Članci

Programiranje

Sharky's Online Vigenere Cipher — Kodiranje i dekodiranje poruka korištenjem poznatog ključa, u web pregledniku (JavaScript)
PyGenere: alat za automatsko dekriptiranje tekstova šifriranih Vigenèreov šifrom (podržano 6 jezika)
Alat za dekriptiranje Vigenèreove šifre.
Perl kod za dešifriranje Vigenèreove šifre
Vigenèreova šifra, implementacija - Izvorni kod u Java i C (GNU GPL)

[1] Smith, Laurence D. (1943). "Substitution Ciphers". Cryptography the Science of Secret Writing: The Science of Secret Writing. Dover Publications. str. 81. ISBN 048620247X

[godina-2] Trithemius je djelo završio 1508. a knjiga je objavljena 1518.

[KahnOrigin-3] 3,0 ^3,1 David, Kahn (1999). "On the Origin of a Species". The Codebreakers: The Story of Secret Writing. Simon & Schuster. ISBN 0684831309

[4] Knudsen, Lars R. (1998). "Block Ciphers— a survey". Unutar Bart Preneel and Vincent Rijmen. State of the Art in Applied Cryptography: Course on Computer Security and Industrial Cryptograph Leuven Belgium, June 1997 Revised Lectures. str. 29. ISBN 3540654747

[5] Codes, Ciphers, & Codebreaking (The Rise Of Field Ciphers)

[6] David, Kahn (1999). "Crises of the Union". The Codebreakers: The Story of Secret Writing. Simon & Schuster. str. 217-221. ISBN 0684831309

[7] Singh, Simon (1999). "Chapter 2: Le Chiffre Indéchiffrable". The Code Book. Anchor Book, Random House. str. 63–78. ISBN 0-385-49532-3

[8] Henk C.A. van Tilborg, ed. (2005). Encyclopedia of Cryptography and Security (First edition ed.). Springer. str. 115. ISBN 038723473X

[9] Mountjoy, Marjorie (1963). "The Bar Statistics". NSA Technical Journal VII (2,4) Published in two parts.

[10] "Lab exercise: Vigenere, RSA, DES, and Authentication Protocols" (PDF). CS 415: Computer and Network Security. http://courses.umass.edu/cs415/labs/lab1/415-lab1-crypto.pdf Pristupljeno 10. studeni 2006.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]