Indeks (baza podataka)

Indeks u bazama podataka je podatkovna struktura koja poboljšava brzinu izvođenja operacija nad tablicom. Obraditi ćemo relacijske baze podataka te ćemo opisati način rada sljedećih indeksa:

• gusti indeksi
• rijetki indeksi
• B+ stablasti indeksi (b+ tree indices)

Prostor na disku koji je potreban za pohranu indeksa je obično mnogo manji nego za tablicu jer indeks sadrži ključna polja. Napravimo analogiju s indeksom u knjigama. Ako želimo pronaći neki pojam u knjizi koristimo indeks knjige koji je sortiran te nakon što pronađemo traženu vrijednost ključ ne listamo stranice u knjizi sekvencijalno već preskočimo odmah do tražene stranice. U bazama podataka umjesto da sustav za upravljanje bazama podataka (SUBP) pretražuje tablicu, koja može imati više od nekoliko desetaka milijuna zapisa, sekvencijalno s namjerom da napravi određenu operaciju dio SUBP-a koji se naziva SQL optimizator koristi indeks nad izvjesnom tablicom kako bi na najučinkovitiji način napravio traženu operaciju.

Traženu vrijednost prvo pretražujemo po indeksu, a tek onda čitamo blokove podataka u kojem se nalazi tražena vrijednost.

Prva struktura indeksa koja će biti obrađena jest nad sortiranim datotekama. Sortirana datoteka jest datoteka u kojoj su zapisi poredani u niz npr. 3, 6, 10, 12, 88 itd. U takvim datotekama n-torke su sortirane po primarnome ključu (i to samo po njemu) te ćemo zbog lakšeg razmatranja pretpostaviti da se radi o cjelobrojnim vrijednostima.

Gusti indeksi

Prva vrsta indeksa koju ćemo opisati jesu gusti indeksi (eng. dense indexes) koji su naziv dobili po tome što je svaka vrijednost iz datoteke reprezentirana u indeksu. Drugim riječima indeks pokazuje na svaki zapis u datoteci. Pretpostavljamo da postoji neki mehanizam brzoga pronalaženja blokova indeksa. Ako je index malen onda ga u cijelosti možemo pohraniti na rezervirani prostor u memoriji te zbog njega nemam skupih I/O operacija na disku, a ako je velik onda možemo nad njim napraviti još jedan sloj indeksa. I/O operacije i razlog zašto su skupe će biti objašnjen kasnije.

Naravno čitatelj bi mogao postaviti pitanje: Pa koja je svrha gradnja indexa nad tablicama te zauzimanje dodatnoga prostora i nad tim indeksima graditi jos jedan sloj indeksa. Razlozi su višestruku:

• Broj blokova indeksa je obično manji u usporedbi s blokovima tablice.
• Budući da su vrijednosti u indeksu sortirane možemo koristiti binarno pretraživanje da bismo pronašli traženu vrijednost. U slučaju gustih indeksa datoteka je sortirana po primarnim ključevima, ali ne mora nužno biti tako. Kako binarno pretraživanje ima logaritamsku složenost vrijeme pretrage je malo.

Primjer 1: Pretpostavimo da imamo tablicu koja u sebi ima milijun zapisa te da koristimo blokove veličine 4096 bitova. Pretpostavimo da u blokove stane deset zapisa. Da bi pretraživali čitavu tablicu morali bismo ju staviti u glavnu memoriju, a ona bi tamo zauzimala više od 400 megabajta. Umjesto izravnoga I/O pristupa koristimo pristup indeksima. Svaki zapis u indeksu se sastoji od ključa koji ima vrijednost i pokazivača na izvjesni zapis u bloku i zovemo ih par ključ-pokazivač. Pretpostavimo da ključevi u indeksima imaju 30 bajtova, a pokazivači na zapise 8. S razumnom količinom zaglavlja bloka možemo staviti 100 pokazivača u 4096 bajtova velik blok. Ako bi koristili gusti indeksi trebali bi samo 10 000 blokova ili 40 megabajta te bi mogli alocirati memoriju za ove blokove. Nadalje za pretraživanje bi koristili binarno pretraživanje te bi trebali pristupiti samo log2(10000) broju blokova što znači da bi bi trebali pristupi 13 ili 14 blokova u potrazi za vrijednošću. Kako binarno pretraživanje pristupa samo manjem skupu blokova te kad i ne bi imali tih 40 megabajta memorije bili bismo u stanju zadržati samo najvažnije blokove u memorije te bi za pristup podacima u memoriji koristili značajno manje nego 14 pristupa disku.

Rijetki indeks

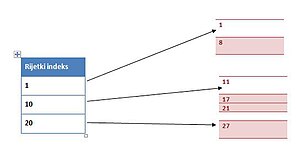
Rijetki indeksi su takva vrsta indeksa gdje indeks pokazuje samo na prvi zapis u bloku. Pretpostavlja se da je datoteka koju pretražujemo sortirana. Kao što vidimo na sljedećoj slici prva četiri ključa u indeksu pokazuju na početak prva četiri bloka. Ako pretpostavimo da imamo milijun blokova podataka, a u svaki blok stane deset zapisa te da sto pokazivača može stati u jedan blok onda bi za korištenje rijetkoga indeksa trebali10 000 blokova podataka.

Stablasti indeksi

Pod stablastim indeksima ovdje mislimo na indekse koji koriste neku strukturu stabla. Mi ćemo ovdje objasniti B + stablo indekse (b-tre indices) indekse njihovu strukturu, način pretraživanja, umetanja i brisanja podataka te samu složenost pojedinih operacija.

Struktura B+ stabla

B+ stablo je balansirana struktura podataka što znači da je svaki put od korijena do listovnoga čvora ista. Svaki čvor b+ stabla se sastoji od n čvorova i n+1 pokazivača. U našem slučaju čvor posjeduje tri ključa i četiri pokazivača.

Primjer 2: Pretpostavimo da imamo 4096 bitova velik blok te da su ključevi 4 bitne, a pokazivači 8 bitne cjelobrojne vrijednosti. Ako nema informacija o zaglavlju onda možemo izračunati broj ključeva i pokazivača za naš blok. Dakle 4n + 8(n + 1) <= 4096 iz čega dobivamo da je n = 340.

Postoje nekoliko važnih pravila koja treba uzeti u obzir: (neka netko uredi ovu sliku meni ne ide :-) )

Indeks prikazan na slici ispod odgovara tablici sa sto milijuna zapisa. Postoji dakle sto milijuna indeksnih zapisa s prosječnom veličinom od 100 bajtova. Uzevši u obzir distribuirani slobodni prostor, postoji 35 redaka po listovnom bloku, a ako SUBP ne skraćuje unutarnje blokove podataka onda je njihova veličina isto 35 zapisa po bloku. Raspored ovih blokova skupa s njihovim veličinama može izgledati kao na slici

• korijen ima barem dva pokazivača koji pokazuju na lijevo odnosno desno podstablo.

• Posljednji pokazivač u bloku pokazuje na sljedeći blok nadesno odnosno na blok s najvećim vrijednostima. Među ostalim pokazivačima barem

$\left\lfloor {\frac {n+1}{2}}\right\rfloor$ se koristi za pokazivanje na zapise, a pokazivači koji ne pokazuju nigdje su null pokazivači.

• Maksimalna razina indeksa koja se koristi jest pet iako ćemo mi u ovdje prezentirati dvorazinsko B+ stablo. Razlog ovome se je prije temeljio na pretpostavci da samo korijenski blok stane u memoriju. Danas kada sve unutrašnji čvorovi stanu u glavnu memoriju, svaka razina indeksa može povećati vrijeme skeniranja indeksa za 50 mikrosekundi. Ako se unutarnji čvor ne nalazi u glavnoj memoriji već u cachu diska, vrijeme može iznositi jednu milisekundu. S druge strane čitanje podataka s diska iznosi 10 milisekundi. (pretpostavili smo da se radi o ovim vremenima i ne moraju nuzno odgovarati realnoj situaciji)

Razine B+ stabla

Indeks dakle sadrži 300 000 4 kilobajtnih blokova što je 12 gigabajta diskovnoga prostora:

• • Prve tri razine su otprilike velike 2500 * 4K = 10 MB te će se oni sigurno nalaziti u međuspremniku
  • Veličina četvrte razine jes 83 000 * 4K što je 332 megabajta. Ako je indeks aktivno korišten on će se nalaziti u cache disk servera (možda 64 gigabajta velikoga) ili u međuspremniku baze podataka (4 gigabajta za indeksne stranice
  • Veličina listovnih stranica iznosi 2,900,000 * 4 K što je skoro 12 gigabajta. Svi indeksni redovi ove razine će biti spremljeni na disku, a za pristup njima trebat ćemo 10 milisekundi.

Jednostavnim računanjem se vidi da pristup bilo kojem redu u ovakvome indeksu treba između 10 i 20 ms čak i ako se radi o neorganiziranim indeksima, a dodavanje nekoga limita na broj razina ipak ima smisla.

Pretraživanje B+ stabla

Ako želimo pronaći vrijednost ključa K indeks pretražujemo rekurizvno počevši u korijenu te završavamo u istome čvoru, a ako se nalazimo u listovnome čvoru, tražimo ključ te čitamo tablicu s diska za željenim zapisom.

Primjer 3: Želimo pronaći vrijednost ključa četiri. Kako se ovdje radi o stablu s dvije razine postupak je trivijalan. Pogledamo je li se tražena vrijednost veća ili manja od 3. Kako je 5 > 4 znači da nam na vrijednost ne pokazuje prvi pokazivač. Gledamo sljedeću vrijednost. 5 > 4 te slijedimo drugi pokazivač. Tu nam se nalazi tražena vrijednost i završili smo s traženjem.

Pretraživanje po intervalu

Pretpostavimo da u tablici imamo ove vrijednosti i želimo napraviti upit

    SELECT  * 
    FROM  tablica 
    WHERE vrijednost  >=  3 AND  vrijednost  <  7;

u kojem tražimo sve vrijednosti između . Prvo što radimo jest da tražimo vrijednost 3 koja se po već objašnjenome postupku nalazi u prvome listovnome čvoru. Prva vrijednost je < 3 pa ju ignoriramo. Druga isto, ali treća je naša tražena vrijednost. Kao što vidimo na slici listovni čvorovi su povezani međusobno i sortirani od manjega prema većemu te jednostavno čitamo vrijednosti slijedno. Sljedeće vrijednosti su 4,5,6, a one sve zadovoljavaju naš uvjet i čitamo ih s diska dok vrijednost 7 ne zadovoljava dani uvjet.