Radijalna distribucijska funkcija: razlika između inačica
Bot: Automatski unos stranica |
m Bot: Automatska zamjena teksta (-{{cite book +{{Citiranje knjige) |
||
| Redak 10: | Redak 10: | ||
<math>g(r) = \frac{\langle n(r)\rangle}{ 4\pi r^2\rho dr} </math> | <math>g(r) = \frac{\langle n(r)\rangle}{ 4\pi r^2\rho dr} </math> | ||
gdje je <math>g(r)</math> radijalna distribucijska funkcija, <math>\langle n(r)\rangle</math> srednji broj čestica, a <math>\rho</math> [[gustoća]]. <ref>L. Zoranić, [http://mapmf.pmfst.unist.hr/~larisaz/md/vjezba2.pdf skripta iz Vježbi za kolegij "Molekularna dinamika"], str. 2</ref> <ref name="HansenMcDonald2005">{{ | gdje je <math>g(r)</math> radijalna distribucijska funkcija, <math>\langle n(r)\rangle</math> srednji broj čestica, a <math>\rho</math> [[gustoća]]. <ref>L. Zoranić, [http://mapmf.pmfst.unist.hr/~larisaz/md/vjezba2.pdf skripta iz Vježbi za kolegij "Molekularna dinamika"], str. 2</ref> <ref name="HansenMcDonald2005">{{Citiranje knjige |author=[[Jean-Pierre Hansen|Hansen, J. P.]] and McDonald, I. R. |year=2005 |title=Theory of Simple Liquids |edition=3rd |publisher=Academic Press}}</ref> | ||
==Definicija== | ==Definicija== | ||
Inačica od 18. studeni 2021. u 01:10
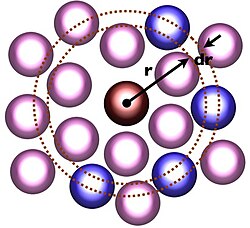
Radijalna distribucijska funkcija (RDF), u statističkoj mehanici, pokazuje kako se mijenja gustoća u odnosu na udaljenost od referentne čestice, u sustavu više čestica. Od iznimne je važnosti za statističku mehaniku i molekularnu dinamiku, s obzirom da povezuje mikroskopske detalje sa makroskopskim svojstvima.
Drugačije iskazano, RDF pokazuje kolika je vjerojatnost da se čestica nađe na nekoj udaljenosti od referentne čestice.
RDF se, tipično, računa tako da se izračunaju udaljenosti između svih parova čestica. Ti podatci se zatim skupe u histogram, koji se normalizira u odnosu na idealni plin (u kojem su čestice totalno nekorelirane).
RDF se može definirati preko srednjeg broja čestica u ljusci debljine na udaljenosti od referentnog atoma, odnosno:
gdje je radijalna distribucijska funkcija, srednji broj čestica, a gustoća. [1] [2]
Definicija
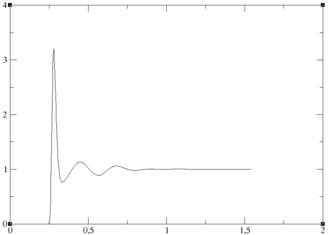
Promotrimo sustav od čestica u volumenu i na temperaturi . Označimo koordinate čestice sa , gdje je . Pošto ne razmatramo situaciju u kojoj na sustav djeluje neko vanjsko polje, potencijalna energija je definirana samo kao interakcija između čestica.
Promatramo kanonski ansambl u kojem je patricijska funkcija definirana kao . Tada je vjerojatnost da se čestica 1 nađe u , čestica 2 u , itd., dana sa jednadžbom
- .
Ukoliko nas zanimaju pozicije manjeg broja čestica, tada možemo fiksirati određen broj čestica , te integrirati prethodni izraz po preostalim koordinatama :
- .
S obzirom da su čestice indentične, više nam odgovara gledati vjerojatnost da bilo koje čestice zauzmu poziciju u bilo kojoj permutaciji - što definira -čestičnu gustoću
Uvođenjem korelacijske funkcije
gdje je jednako , a ispravlja korelaciju između atoma, dolazimo do konačne relacije:
Izvori
- ↑ L. Zoranić, skripta iz Vježbi za kolegij "Molekularna dinamika", str. 2
- ↑ Hansen, J. P. and McDonald, I. R. (2005) Theory of Simple Liquids.



























